Assalamualaikum gan, alhamdullilah ada waktu senggang buat posting soal dan pembahasan soal matematika part 2 terusan dari seri yang kemarin, sebelumnya di postingan kali ini aku akan membahas soal UN Matematika IPA tahun 2018 secara lengkap , jelas, dan detail !!. Dipertemuan kemarin aku baru ngebahas soal 1 sampai 10, dan di postingan ini akan aku bahas nomor 11 sampai 20, yap langsung saja :
Baca Juga : Pembahasan Bocoran Soal UN Matematika SMA IPA 2018 Lengkap
Untuk soalnya saya dapat dari blog pak anang : (http://pak-anang.blogspot.com/2018/04/bocoran-soal-un-matematika-sma-ipa-2018.html) . Ini soalnya, agan dapat mendownload di link dibawah ini :
Download Soal UN
Soal dan pembahasan nya (Warna merah soalnya) :
11. Interval nilai p yang menyebabkan fungsi kuadrat f(x) = px2 - (2p + 3)x + p + 2 definit
negatif adalah ...
jawab :
Definit negatif artinya selalu negatif, dan grafiknya dibawah sumbu x. Dengan demikian
karena definit negatif maka a < 0 dan D < 0 . Dari rumus itu maka p < 0 .
Dari f(x) = px2 - (2p + 3)x + p + 2 diketahui :
a = p
b = - (2p + 3)
c = p + 2
Pembahasan :
D < 0
b2 - 4ac < 0
( - (2p + 3))2 - 4p(p + 2) < 0
4p2 + 12p + 9 - 4p2 - 8p < 0
4p + 9 < 0
4p < - 9
p < -9/4
Maka didapatkan jawabannya : p < -9/4
12. Uang Adi Rp60.000,00 lebih banyak dari uang Deni ditambah dua kali uang Riski.
Jumlah uang Adi, Deni, dan Riski adalah Rp300.000,00. Selisih uang Deni dan Riski
adalah Rp15.000,00. Uang Adi adalah ....
jawab :
Diketahui :
A = Adi
D = Deni
R = Riski
Kita buat terlebih dahulu persamaan-persamaan dengan memahami soal diatas :
Persamaan 1 : A - (D + 2R) = 60.000
Persamaan 2 : A + D + R = 300.000
Persamaan 3 : D - R = 15.000
Eliminasi variabel D :
A - D - 2R = 60.000
A + D + R = 300.000
--------------------------- +
2A - R = 360.000 (Persamaan 4)
Ubah Persamaan 3 :
D - R = 15.000
R = D - 15.000 (Persamaan 5)
Masukkan persamaan 5 ke persamaan 4 :
2A - R = 360.000
2A - (D - 15.000) = 360.000
2A = 360.000 + (D - 15.000)
2A = 345.000 + D (Persamaan 6)
Masukkan persamaan 5 ke persamaan 2 agar tereliminasi R nya :
A + D + R = 300.000
A + D + (D - 15.000) = 300.000
A + 2D - 15.000 = 300.000
2D = 315.000 - A
D = (315.000 - A) / 2 (Persamaan 7)
Masukkan persamaan 7 ke persamaan 6 :
2A = 345.000 + D
2A = 345.000 + (315.000 - A) / 2
Dikalikan 2 agar tidak ada yang pecahan :
4A = 690.000 + 315.000 - A
5A = 1.005.000
A = 201.000
Jadi Uang Adi = Rp. 201.000
13. Luas daerah parkir 1.760 m2. Luas rata-rata untuk mobil kecil 4 m2 dan mobil besar 20 m2.
Daya tampung maksimum hanya 200 kendaraan, biaya parkir mobil kecil Rp1.000,00/jam dan
mobil besar Rp2.000,00/jam. Jika dalam satu jam terisi penuh dan tidak kendaraan yang pergi
dan datang, maka hasil maksimum tempat parkir itu adalah ....
Jawab :
Misalnya :
x = mobil kecil
y = mobil besar
Diketahui dari soal :
4x + 20y = 1760
x + y = 200
Eliminasi x :
4x + 20y = 1760 dibagi 4
x + y = 200
x + 5y = 440
x + y = 200
------------------ -
4y = 240
y = 60
Substitusikan :
x + y = 200
x + 60 = 200
x = 200 - 60
x = 140
Didapatkan jumlah maksimal mobil kecil = 140 dan mobil besar = 60
Biaya parkir mobil kecil : 1000
Biaya parkir mobil besar : 2000
Maka tinggal dikalikan :
140*1000 + 60*2000 = Rp 140.000 + Rp 120.000
= Rp. 260.000
14. Diketahui matriks-matriks :
Jika BT adalah transpose dari matriks B, dan
Jawab :
Kita Transpose kan dulu matriks B :
(2x - 3z) + 2 - 2 = 3 Persamaan dari ordo ke-1
(z - 3) - 1 - (-9) = 4 Persamaan dari ordo ke-3
9 + (z - 4) - y = 6 Persamaan dari ordo ke-4
Mari kita sederhanakan :
2x - 3z = 3 Hasil penyederhanaan persamaan ordo ke-1
z = -1 Hasil penyederhanaan persamaan ordo ke-3
z - y = 1 Hasil penyederhanaan persamaan ordo ke-4
Substitusikan dengan memasukan nilai z ke persamaan 2x - 3z = 3 ,yaitu :
2x - 3z = 3
2x - 3(-1) = 3
2x + 3 = 3
2x = 3 - 3
x = 0
Substitusikan dengan memasukan nilai z ke persamaan z - y = 1 ,yaitu :
z - y = 1
-1 - y = 1
- y = 1 + 1
-y = 2
y = -2
Dengan demikian didapat : x = 0 , y = -2, dan z = -1
Jadi nilai x + y + z = 0 - 2 - 1 = -3
15. Diketahui matriks :
C = AB. Invers dari matriks C adalah ...
Jawab :
Rumus perkalian matriks :
16. Di sebuah toko bahan bangunan terdapat tumpukan batu bata. Banyak batu bata pada
tumpukan paling atas adalah 12 buah dan selalu bertambah 2 buah pada tumpukan di
bawahnya. Jika terdapat 40 tumpukan batu bata dari tumpukan bagian atas sampai bawah
dan harga setiap batu bata adalah Rp600,00, maka besarnya biaya yang harus dikeluarkan
untuk membeli seluruhnya adalah ....
Jawab :
[Bab Baris dan Deret]
Dari soal diatas kita menggunakan rumus jumlah suku ke-n , rumusnya yaitu :
n = jumlah ke berapa yang akan kita cari
a = suku pertama
b = beda
Dengan demikian, diketahui :
n = 40
a = 12
b = 2
Perhitungannya :
Karena yang ditanya besarnya biaya yang harus dikeluarkan untuk membeli seluruhnya maka :
S40 x Rp.600 = 2040 x Rp.600
= Rp.1.224.000
17. Suku ke-n suatu barisan geometri adalah Un = 4n . Jumlah n suku pertama dari barisan
geometri tersebut adalah ...
Jawab :
Rumus yang akan kita gunakan :
Mencari suku ke-n (Geometri) : Un = arn-1
Mencari jumlah suku ke-n (Geometri) :
a = suku pertama
r = rasio
Perhitungannya :
Cari nilai a terlebih dahulu :
Dari soal : Un = 4n
U1 = 41
U1 = 4
U1 bisa juga disebut a (U1 = a) , itu berarti a = 4.
Kita cari nilai r nya :
Un = 4n
U2 = 42
U2 = 16
Un = arn-1
U2 = 4r2-1
16 = 4r1
r = 4
Didapatkan nilai a = 4 dan r = 4. Diketahui r = 4, itu berarti r > 1. Maka kita
menggunakan rumus yang ini :
18. Nilai dari :
Jawab :
19. Nilai dari
Rumus cara cepat :
Pembahasannya :
Setelah berhasil dibuat untuk memenuhi syarat perhitungan cara cepat, maka
kita tinggal memasukkan kedalam rumus cara cepat diatas.
Diketahui dari hasil diatas:
b = -6
q = 12
a = 9
Jika dimasukkan ke rumus maka :
20. Sebuah tabung tanpa tutup yang terbuat dari lempengan tipis dapat memuat minyak tanah
sebanyak 8π cm3. Luas minimum permukaan tabung adalah ....
Jawab :
Perlu di ketahui :
La = Luas Alas
Ls = Luas Selimut Tabung
Kl = Keliling Lingkaran
Lp = Luas Permukaan Tabung
Perhitungan :
V = 8π cm3
Lp = La + Ls
Lp = πr 2 + Kl . t
= πr 2 + 2 πr . t
= πr(r + 2t)
V = πr 2t
t = V / (πr 2)
= 8π / (πr 2)
= 8 / r 2
Substitusikan t nya ke rumus Lp , maka :
Lp = πr 2 + 2 πr . (8 / r 2)
= πr 2 + 16 πr -1
Lp' = 2 πr - 16 πr -2 = 0
2 πr = 16 πr -2
r 3 = 16π / 2π
= 8
r = 2
t = 8 / r 2
Masukkan nilai r
t = 8 / 22
= 2
Lp = πr(r + 2t)
= π2 (2 + 2.2)
= 2π (6)
= 12π
Jadi, Luas minimum permukaan tabung adalah 12π
Terimakasih telah berkunjung :D , part selanjutnya menyusul.
Bagikan
Part 2 : Pembahasan Bocoran Soal UN Matematika SMA IPA 2018 Lengkap
4/
5
Oleh
Bayu Ambika
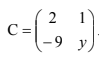
Silahkan berkomentar secara bijak dan sesuai dengan topik pembahasan ...
Untuk menyisipkan kode pendek, gunakan <i rel="code"> ... KODE ... </i>
Untuk menyisipkan kode panjang, gunakan <i rel="pre"> ... KODE ... </i>
Untuk menyisipkan gambar, gunakan <i rel="image"> ... URL GAMBAR ... </i>